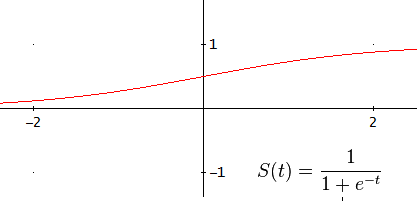Definition
An MLP (Multilayer perceptron) is a feedforward neural network which consists of many perceptrons joined in many layers. The most basic MLP has 3 layers: one input layer, one output layer and one hidden layer, but it may have as many hidden layers as necessary. Each individual layer may contain a different number of neurons.
[latex]
W_1 = \begin{bmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{bmatrix}
\quad
W_2 = \begin{bmatrix}
.. & .. & .. & ..
\end{bmatrix}
[/latex]
Feedforward means that nodes have a direct connection such that nodes located in between are fed by the outputs of previous nodes and so on. This is very simple to program because it is basically as the perceptron: multiply weights (including bias nodes) by the input vector, give the result to the activation function, and the output will be the input of the next layer until the output layer is reached.
In the entry about the perceptron I used the step function as the activation function, but in MLP a variety of them can be used. Most of them are sigmoid (mathematical functions having an “S” shape) such as:
The difference between these two sigmoids is that the hyperbolic tangent goes from -1 to 1 whereas the other goes from 0 to 1.
Sometimes linear functions are also needed for cases when neural networks are not used for classification but for extrapolation and any kind of prediction.
If the MLP misclassifies an input, it is necessary to back-propagate the error rate through the neural network in order to update old weights. Gradient descent through derivatives is used to correct the weights as much as possible. Derivatives show how the error varies depending on the weights to later apply the proper correction.
In perceptrons, the error function was basically [latex]t_i – y_i[/latex] (desired output minus system’s output) but in MLP the squared error function will be used instead [latex]J = \sum \frac{1}{2}(y-\widehat{y})^2[/latex]:
- It has a sum because each element has its own error and it is necessary to sum them up.
- It is squared because convex functions’ local and global minima are the same.
- It has a [latex]\frac{1}{2}[/latex] to make it simpler when obtaining the derivative.
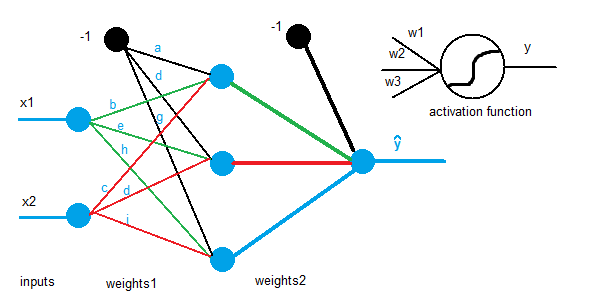
The following mathematical explanation regarding the formulas for the learning process is based on the 2x3x1 neural network depicted in the first picture of the entry, but before that, some terms need to be introduced to avoid misunderstandings:
[latex]X \to [/latex] Input matrix.
[latex]W_1 \to [/latex] Weights’ matrix that connects the input and hidden layers.
[latex]W_2 \to [/latex] Weights’ matrix that connects the hidden and output layers.
[latex]y \to [/latex] Desired output.
[latex]\eta \to [/latex] Learning rate.
[latex]z_2 = x*W_1 \to [/latex] Content of each node in the hidden layer (before activation).
[latex]a_2 = f(z_2) \to [/latex] Content of each node in the hidden layer (after activation).
[latex]z_3 = a_2*W_2 \to [/latex] Content of each node in the output layer (before activation).
[latex]\widehat{y} = f(z_3) \to [/latex] MLP output.
[latex]J = \sum \frac{1}{2}(y-\widehat{y})^2 \to [/latex] Squared error function.
First, let us calculate the update formula for [latex]W_2[/latex]. For this, it is necessary to calculate the derivative of the error with respect to [latex]W_2[/latex] to see how much the error varies depending on [latex]W_2[/latex].
[latex]\frac{\partial J}{\partial W_2} = \frac{\partial \sum \frac{1}{2} (y – \widehat{y})^2}{\partial W_2} = \sum \frac{\partial \frac{1}{2} (y – \widehat{y})^2}{\partial W_2}
[/latex]
By the sum rule in differentiation we can take the sum off the fraction, and from now on it is no longer needed since at the end we can sum each sample individually, so let us derive it.
[latex]\frac{1}{2} \cdot 2 \cdot (y – \widehat{y}) \cdot [ \frac{\partial y}{\partial W_2} – \frac{\partial \widehat{y}}{\partial W_2} ][/latex]
The derivative of y with respect to [latex]W_2[/latex] is 0 since y does not depend on [latex]W_2[/latex].
[latex]-1 (y – \widehat{y}) \cdot \frac{\partial \widehat{y}}{\partial W_2}[/latex]
By applying the chain rule:
[latex]-1 (y – \widehat{y}) \cdot \frac{\partial \widehat{y}}{\partial z_3} \cdot \frac{\partial z_3}{\partial W_2}[/latex]
Which finally:
[latex]-1 (y – \widehat{y}) f'(z_3) \cdot a_2 \to \delta_3[/latex]
In case of [latex]W_1[/latex] the procedure is very similar:
[latex]\frac{\partial J}{W_1} = [\text{same things…} ] = \delta_3 \cdot \frac{\partial z_3}{\partial W_1} = \delta_3 \cdot \frac{\partial z_3}{\partial a_2} \cdot \frac{\partial a_2}{\partial W_1} \\
= \delta_3 \cdot W_2 \cdot \frac{\partial a_2}{\partial z_2} \cdot \frac{\partial z_2}{\partial W_1} = \delta_3 \cdot W_2 \cdot f'(z_2) \cdot x[/latex]
Learning process (update rules):
[latex]W_1 = W_1 + \eta \frac{\partial J}{\partial W_1} \\
W_2 = W_2 + \eta \frac{\partial J}{\partial W_2}[/latex]
Results
The MLP I developed was able to correctly classify samples from its training set from 3 different classes. I have not written a word about overfitting because I will probably do that in a different entry with a good solution to overcome it, but this algorithm probably overfits and cannot classify other samples with the same good result.
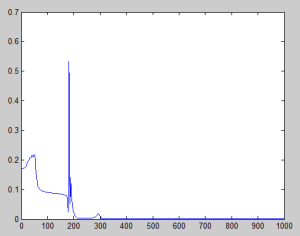
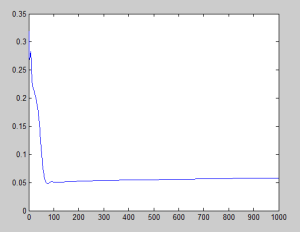
Finally, I recorded the evolution of the error with two different learning rate to show that if [latex]\eta[/latex] is too big, it can escape from the minimum with an unknown result. In this case, it resulted absolutely good, but it is not always the case.
Left: [latex]\eta = -0.2[/latex]. Right: [latex]\eta = -0.1[/latex]
The code is provided in the Source code section.
References
I strongly recommend the set of videos to which this one belongs to.