The chain rule in Tensorflow

Manipulating any type of neural network involves dealing with the backpropagation algorithm and thus it is key to understand concepts such as derivatives, chain rule, gradients, etc. It is often important to not only theoretically understand them but also being able to play around with them, and that is the goal of this post. Most of the information presented has been collected from different posts from stackoverflow.

There are three types of differentiation:

• Numerical: it uses the definition of the derivative (lim) to approximate the result.
• Symbolic: manipulation of mathematical expressions (the one we learn in high school).
• Automatic: repeatedly using the chain rule to break down the expression and use simple rules to obtain the result.

As the author of the answer (Salvador Dali) in stackoverflow points out, symbolic and automatic differentiation look similar but they are different.

Tensorflow uses reverse mode automatic differentiation.

As mentioned above, Automatic differentiation uses the chain rule so there are two possible ways to apply it: from inside to outside (forward mode) and vice versa (reverse mode). In the Automatic differentiation Wikipedia page there are a couple of step-by-step examples of forward and reverse mode quite easy to follow. The reverse mode is a bit harder to see probably because of the notation introduced by the Wikipedia but someone made a simple decomposition easier to understand.

Gradients

Gradients of common mathematical operations are included in Tensorflow so they can be directly applied during the reverse mode automatic differentiation process. In fact, if you want to implement a new operation it has to inherit from Decop and its gradient has to be “registered” (RegisterGradient). For example, this is how the derivative of [latex s=2]f(x)=sin(x)[/latex] looks like (python/ops/math_grad.py):

The function tf.gradients is used by any optimizer because they all inherit from the class Optimizer (python/training/optimizer.py). tf.gradients is not commonly used directly but it is implicitly used when calling the function minimize as:

More specifically, “minimize” function has two tasks:

1. Calculate gradients
2. Apply gradients

We can thus apply those operations, or even break down calculate_gradients to use tf.gradients. Here there are three alternatives when minimizing a loss function:

This decomposition of the function minimize can be useful in some cases. For instance, you may want to process or keep track of the gradients to understand the Graph computations or you may want to calculate the gradients with respect to only some variables and not all of them.

Simple tf.gradients example

We have the function [latex s=2]z = f(x,y) = 2x-y[/latex] and we want to calculate both of its partial derivatives [latex s=2]\frac{\partial z}{\partial x} = 2[/latex] and [latex s=2]\frac{\partial z}{\partial y} = -1[/latex].

In the previous example we could not see that after the derivatives are calculated, tf.gradients also substitutes each variable by its value and performs the corresponding calculations. Another example: [latex s=2]z = f(x,y) = sin(x)-y^3[/latex]. [latex s=2]\frac{\partial z}{\partial x} = cos(x)[/latex], [latex s=2]\frac{\partial z}{\partial y} = -3y^2[/latex]

Dropout

Dropout [1] is an incredibly popular method to combat overfitting in neural networks. The idea behind Dropout is to approximate an exponential number of models to combine them and predict the output. In machine learning it has been proven the good performance of combining different models to tackle a problem (i.e. AdaBoost), or combining models trained in different parts of the dataset. However, when it comes to deep learning, this becomes too expensive, and Dropout is a technique to approximate this.

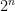Dropout can be easily implemented by randomly disconnecting some neurons of the network, resulting in what is called a “thinned” network. Thus, if the model has [latex]n[/latex] neurons, there are [latex]2^n[/latex] potential models. Each of them might be trained once or few times, or even not trained at all. Generating one of these random models is done batch-wise so in every batch there will be a new dropout mask (to disconnect the corresponding weights) generated. At train time, each neuron has a probably [latex]p[/latex] of being disconnected. For instance, if [latex]p=0.5[/latex] (recommended configuration, except for the input layer which is recommended to have [latex]p=0.8[/latex]) and we have 200 neurons, the first batch might encounter 90 activated neurons, the second batch might encounter 103 activated neurons, etc.

At test time, all neurons will multiply [latex]p[/latex].

In the image above we can see a simple implementation of a standard feedforward pass: weights multiply inputs, add bias, and pass it to the activation function. The second set of formulas describe how it would look like if we add dropout:

1. Generate a dropout mask: Bernoulli random variables (i.e. 1.0*(np.random.random((size))>p)
2. Apply the mask to the inputs disconnecting some neurons.
3. Use this new layer to multiply weights and add bias
4. Finally use the activation function.

All the weights are shared across the potential exponential number of networks, and during backpropagation, only the weights of the “thinned network” will be updated.

How is it implemented in Tensorflow?

In Tensorflow it is implemented in a different way that seems to be equivalent. Let’s have a look at the following example. According to the paper:

Let our neurons be: [latex][1,2,3,4,5,6,7,8][/latex] with [latex]p=0.5[/latex].
At train time, half of the neurons would be randomly disconnected, leading to [latex][1,0,0,4,5,0,7,0][/latex]
At test time, we would have multiplied the whole matrix by p, leading to [latex]0.5*[1,2,3,4,5,6,7,8][/latex]

In other words, we downgrade the outcome at testing time. In contrast, in Tensorflow, we do it the other way around. We increase the values at training time by [latex]1/prob[/latex]. Following our example:

Let our neurons be: [latex][1,2,3,4,5,6,7,8][/latex] with [latex]p=0.5[/latex].
At train time, half of the neurons are randomly disconnected, leading to [latex]1/0.5*[1,0,0,4,5,0,7,0] = [2,0,0,8,5,0,14,0][/latex]
At test time, we would use 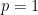[latex]p=1[/latex], leading to [latex]1/1*[1,2,3,4,5,6,7,8][/latex]

In other words, at testing time we treat it as a normal neural network without dropout, and at training time we upscale the values by [latex]1/prob[/latex].

The reason why the values are upscale is to preserve the total sum (approx.).

[latex]sum([1,2,3,4,5,6,7,8]) = 36[/latex]
[latex]sum(1/0.5 * [1,0,0,4,5,0,7,0]) = 29[/latex]

This makes sense because if our layer produces certain output, we want to keep it approximately the same regardless of any method we are using to combat overfitting.

Dropout in Tensorflow

Adding a dropout layer in Tensorflow is really easy.

Where current_keep_prob will be [latex]p[/latex] during training time and 1 during inference/testing time.

As I mentioned before, only those weights that were successfully masked (without the ones corresponding to the dropped out neurons) will be updated. If I have 100 neurons and [latex]p=0.5[/latex], half of the weights are expected to be updated. In the gif below we can see the evolution of 3 different plots: the first shows how the weights are being updated, the second shows which weights are being updated and the third is a cumulative sum of the second.

Optimizers comparison with and without Dropout

Due to the nature of AdamOptimizer, it does not follow this rule of updating only the weights belonging to the “thinned” network, so I found interesting to compare the performance of several optimizers in a simple neural network.

Test
Goal: To perform a first step to check the performance between Adam, Adadelta, Adagrad and Gradient Descent across different learning rates (1000 learning rates between 1e-6 to 1e-1).
Dataset: EMNIST (47 classes).
Batch size: 8.
Epochs: 1.
Network: conv2d (3,3,1,32), conv2d (3,3,32,64), max pooling (2,2), reshape (12*12*64), dense (12*12*64,128), dense (128,47).
Weights initialization: he_uniform. Bias initialization: zeros.
Activation layers: ReLU (and softmax at the end of the network).
Cost function: cross entropy.

These graph does not show the actual performance of dropout under each optimizer since I only tested a bunch of learning rates without properly examine and focus where it seems to provide good results. In addition, it is not fair to compare on the same learning rates dropout vs non-dropout. Instead, this shows how a first step looks like .

References

1. NNitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, Ruslan Salakhutdinov. 2014. “Dropout: A simple way to prevent neural networks from overfitting”