Tag: Gaussian blur

[Image Processing] Gaussian blur

Juan Miguel Valverde 2 Comments

Definition

Gaussian blur is used in image processing to blur images. In most of the cases, this is done with the sole purpose of removing noise, but it is also necessary to take some care to its two different parameters. Depending on this two parameters, the result will vary. These two parameters are the size of the kernel and sigma.

In order to calculate the kernel that will be used to convolve the picture, we need to use the Gaussian formula for two dimensions, which is the following:

[latex]
G(x,y) = \frac{1}{2 \pi \sigma ^2} e ^{- \frac{x^2 + y^2}{2 \sigma ^2}}
[/latex]

Let us say that we want to generate a kernel of size 7 with [latex]\sigma = 0.84089642[/latex].
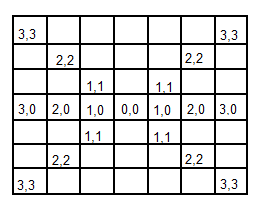
X and Y values are determined by the position of each element in the matrix.

positions

Finally, the values are:

0.00000067 0.00002292 0.00019117 0.00038771 0.00019117 0.00002292 0.00000067
0.00002292 0.00078634 0.00655965 0.01330373 0.00655965 0.00078633 0.00002292
0.00019117 0.00655965 0.05472157 0.11098164 0.05472157 0.00655965 0.00019117
0.00038771 0.01330373 0.11098164 0.22508352 0.11098164 0.01330373 0.00038771
0.00019117 0.00655965 0.05472157 0.11098164 0.05472157 0.00655965 0.00019117
0.00002292 0.00078634 0.00655965 0.01330373 0.00655965 0.00078633 0.00002292
0.00000067 0.00002292 0.00019117 0.00038771 0.00019117 0.00002292 0.00000067

The algorithm may be something like this:

Given kernel’s size and [latex]\sigma[/latex] generate a kernel
Iterate over rows
Iterate over columns
Convolve the windowed region with the generated kernel
Write that value on the output picture

Results

blur0

Original
gauss1

[latex]\sigma = 0.84089642[/latex], kernel’s size = 7
gauss2

[latex]\sigma = 1.5[/latex], kernel’s size = 7
gauss3

[latex]\sigma = 1.5[/latex], kernel’s size = 3

To make it easier, I used a black and white picture, but for color pictures we just need to do the same through the different channels.
It is possible to avoid the darkening of the images by normalizing output pixels during the process.

References

1. M. Nixon and A. Aguado. 2008. “First order edge detection operators”, Feature Extraction & Image Processing.
2. Wikipedia, http://en.wikipedia.org/wiki/Gaussian_blur