[Hough Transform] Ellipse detection and space reduction

This is the last entry regarding Hough Transform. I previously wrote about Line Detection and Circle Detection including some Source Code, but in this case I will just write about it. The reason why I did not write any code is because it can be found in [1] and because it is very similar to the Circle Detector.

Brief Introduction

Ellipse detection is another useful tool that may have various applications in the field of recognition. Let us not forget that sometimes due to the movement when a picture is taken, in some images circles cannot be represented correctly, so ellipses appear instead. Ellipses are also a very simple shape that can be interesting to recognize since we live surrounded by objects with that shape. As an example, self-driving cars are intended to recognize traffic signs. In particular, rounded traffic signs may look elliptical when they are seen from a specific point of view.

Simple way (5 dimensions)

This approach is very similar to the Circle Detector. Circumferences have 3 characteristics needed to be defined: radius and center coordinates. Likewise, it can be said that in case of ellipses we need 5 characteristics: the center (2), the size along both axes (2) and its rotation (1).

Implementing a 5 dimensional matrix will lead us to fall over the curse of dimensionality. This approach can be reasonable when the algorithm faces a known environment and therefore some characteristics can be drastically reduced. For instance, if a fixed camera aims to capture the movement of the moon, the size of its radius will not change very much, and as the movement can also be predicted, one can simply modify a few parameters to adapt the algorithm and focus on a certain region.

The implementation, as stated above, is similar to the circle detector: using the trigonometric characteristics of the ellipse one can establish relationships between them and iterate over each parameter to try all combinations along the whole image. There is a Matlab code written in [1] (page 209).

Space Reduction

Space reduction is applied in a very similar way to the Circle Detector. Nonetheless, as ellipses are figures a bit more complex than circumferences, it can be more problematic to achieve the solution. Let us recall that for circumferences, it is only necessary to take the center point in the chord between two prospective points that might belong to the circumference, and draw a perpendicular line to the chord passing through the center point. This is possible due to the orthogonality between these two lines, but this is not the case when analyzing ellipses. The equivalent to that perpendicular line in the circumference must be found in other way, for instance, using the tangential lines of those two chosen points, as we can see below.

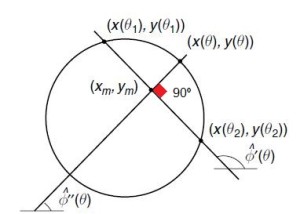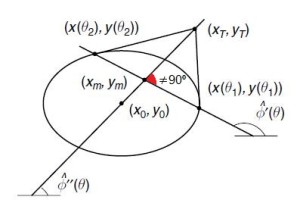Circle detection		Ellipse detection

The algorithm shown in the book [1] is similar to the Circle detector: it iterates over the whole picture trying to find a black pixel. When it is detected, it looks in the neighborhood for another one to draw a chord and therefore, the pixel in the center of the chord. The proposed way to find the coordinates of the pixel out of the ellipse is by the intersection of the tangent of those two chosen points. The author proposed that these tangents can be obtained before the process of Non-Maximum Suppression. In this case, during the use of Sobel filter the angles to generate those tangents can be obtained when Canny Edge detector is used.

Finally, we just need to obtain the maxima of the accumulator, and draw the consequent ellipse.

References

1. M. Nixon and A. Aguado. 2008. “First order edge detection operators”, Feature Extraction & Image Processing.