Definitions
Sarsa is one of the most well-known Temporal Difference algorithms used in Reinforcement Learning. TD algorithms combine Monte Carlo ideas, in that it can learn from raw experience without a model of the environment’s dynamics, with Dynamic Programming ideas, in that their learned estimates are based on previous estimates without the need of waiting for a final outcome [1].
On-policy methods learn the value of the policy that is being used to make decisions, whereas off-policy methods learn from different policies for behavior and estimation [2].
Sarsa algorithm
On the contrary of other RL methods that are mathematically proved to converge, TD convergence depends on the learning rate α. In order to understand this, we only need to imagine the typical downhill image that comes to our minds when dealing with learning rates. If the chosen learning rate is not small enough, the error will go downhill but at some point it will go uphill. As we will see on the simulations I carried on, this may have devastating consequences as messing up the final result. Nonetheless, if the learning rate is not big enough, it won’t reach the optimal solution if we don’t iterate enough.
The algorithm is quite simple, but it’s important to understand it.
Repeat (for each episode):
Initialize s
Choose a from s using a policy derived from Q (e.g., ɛ-greedy)
Repeat (for each step of the episode):
Take action a, observe r, s'
Choose a' from s' using policy derived from Q (e.g., ɛ-greedy)
Q (s,a) ← Q(s,a) + α[r + γQ(s',a') - Q(s,a)]
s ← s'; a ← a'
until s is terminal
α represents the learning rate, how much does the algorithm learn each iteration.
γ represents the discounted reward, how important is the next state.
r is the reward the algorithm gets after performing action a from state s leading to state s’.
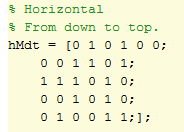
Q(s,a) stores the value of doing action a from state s. There will be 36 states and 4 different actions (1 = going up, 2 = left, 3 = down, 4 = right).
I reused the code of my previous simulation [Reinforcement Learning] First-visit Monte Carlo simulation solving a maze. To make it faster I avoided the GUI, however, it can be turned on by simply change a parameter from 0 to 1.
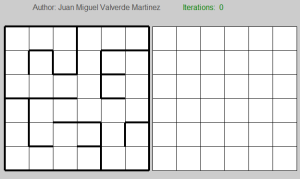
Since I am not using a graphical interface, it is worth mentioning that the numbers in the first grid represent the states, so for this maze, the optimal solution will be: 1 – 7 – 13 – 14 – 15 – 16 – 22 – 23 – 29 – 35 – 36
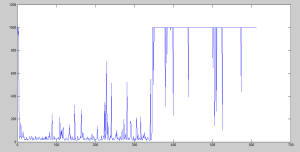
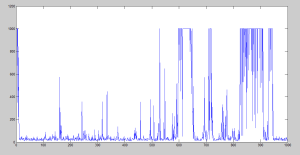
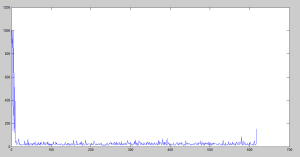
The algorithm has a certain number of iterations that will allow us to control how far it is going to iterate. I also established a limit of iterations for each general iteration to avoid getting stuck. In all cases I tried with γ = 1, so I consider really important the next state. In contrast, I tried with different learning rates.
We can clearly see that it starts with many iterations, but it decreases very soon. However, after it starts increasing the iterations, it gets worse and worse. We can actually see that it surpassed the limit of 1000 iterations many times.
Here it is slightly better, but still terribly bad after the 150th iteration approx.
We can finally see here that the performance is way better, but still it gets worse after 875th iteration. Nonetheless, what is it being done when it starts to grow up again? In terms of the amount of iterations, we can see that peak here:
If we check what is going on in the state transition, we will find that it is stuck and it will be stuck until a random number lower than ɛ is generated, and therefore, try another solution.
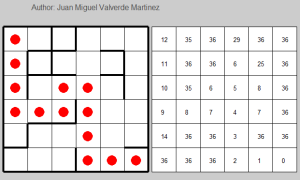
When it starts to get worse, we can stop the general iteration and check the S(a,b) values to understand what happens.
From state 8, the only option the algorithm can perform is doing the third action (going down).
From state 14, the best option is the action number 1, which means going up. Note that the correct action (left) is slightly worse: 1.752 – 1.7498 = 0.0022. Note also that that amount is smaller than the learning rate 0.01. If it learns again the correct answer, it will be fixed.
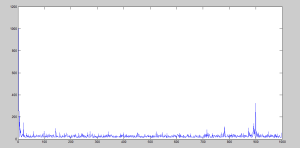
The final solution to this problem was using the following parameters:
α = 0.1;
γ = 1;
maxCounter = 700; % Limit of general iterations
And a small trick: after the 20th general iteration it usually starts to get better, so I will add a small piece of code to tell the algorithm that if it starts to get worse after the 20th iteration, it should stop automatically before it completely messes up the solution.
finish = 1;
end
Demonstration:
Complementary slides explaining the algorithm: Sarsa Algorithm
References
1. R. S. Sutton and A. G. Barto. 2005. “Temporal-Difference Learning”, Reinforcement Learning: An Introduction. (http://webdocs.cs.ualberta.ca/~sutton/book/ebook/node60.html)
2. http://www.cse.unsw.edu.au/~cs9417ml/RL1/tdlearning.html